Introduction to Real sequences; convergent, divergent and oscillating real sequences

First, let's try to understand what sequences really are. So formally, "A sequence in a non-empty set A is a function from ℕ into A."

In particular, a real sequence 'a' is a function from ℕ into ℝ.

                                                                i.e., a: ℕ →  ℝ.

The n^th term of the sequence is denoted by a_n. Since a sequence is fully described by describing a_n for each n ∈ ℕ, some of the ways in which we denote a sequence are: 

VISUAL REPRESENTATION

Imagine a red dot flashing, first at a₁, then a₂ and a₃ and so on. 

The dots keep on moving until it disappears, i.e., it moves towards infinity for the sequence of natural numbers. 

So, the ordering of the flashes determines the order of the sequence.

                        

Some cool examples of sequences include the famous Fibonacci sequence, which is usually denoted by F_n. Each term of the sequence is the sum of the two preceding terms, starting from 0 and 1.

Now, something very interesting happens if you create a new sequence by dividing each term of F_n by the term preceding it:

1 / 1 = 1 

2 / 1 = 2

3 / 2 = 1.5

5/ 3 = 1.667 

8 / 5 = 1.6 

13 / 8 = 1.625

21 / 13 = 1.615

34 / 21 = 1.619

55 / 34 = 1.618

We can see that each subsequent number in this sequence is approaching or getting closer and closer to the "Golden Ratio". This concept of sequences approaching a finite real number will be discussed later.

You'll be surprised to know that sequences can even be used to calculate the area of geometrical figures. For example, Euclid calculated the area of a circle  A=πr² by using sequences. He started by inscribing a square inside the circle and then doubled the number of sides to get an octagon, doubled again to get a 16-gon, and so forth. The area of each polygon was an approximation to the area of the circle, the error being the area outside the polygon. He showed that error was decreased by more than half with each doubling of magnitude.

This is a sequence of polygons, and the areas of the polygons form a sequence of real numbers. Later, Archimedes used this method to find an approximation to π. The only difference was that he used a hexagon instead of a square.

It's interesting to see that we can comprehend sequences in this manner. As you must have observed in the above examples, that sequences were converging to a finite real number. This phenomenon of sequences is called "convergence".

We can try to describe this behavior of a sequence whose terms appear to come very close to some l ∈ ℝ  and we will refer to this symbolically as a_n →l as n →∞.

Now, let’s try to see how students from different majors would describe this phenomenon!

For someone majoring in English, they would probably say that the terms of the sequence come very close to l eventually.

For someone interested in Economics, they would say a_n can be brought arbitrarily close to l provided that n is sufficiently large.

For a physics major, they would say a_n can be brought infinitesimally close to l provided n is infinitely large. 

For a Maths major,  they would say that for every open interval I centered at l, there exists n₀ ∈ ℕ such that all the terms after a_n0 will lie in that open interval. We can say that for every such open interval there will exist some n₀ after which the tail of the sequence will lie in that interval. This n₀ will keep changing with I. 

Hence, now we can define convergence formally.

Thus, a_n is said to converge to a real number l iff ∀ ε > 0, ∃ n₀ ∈ ℕ such that n ≥ n₀ ⟹ 

|a_n - l|< ε ⟺ l - ε < a_n < l + ε ⟺ a_n  ∈  I ε(l).

During the visual representation of sequences, we observed that the sequence of natural numbers does not approach a finite real number and it seems to tend to infinity. Thus, it does not fit the definition of convergence. This phenomenon of sequences tending to infinity is termed as "divergence".

If we try to define the divergence of a sequence we will need the concept of infinity, i.e., sequences diverging to ∞ would mean a_n→∞ as n →∞.

By the above definition of convergence, we know that a_n can be arbitrarily close to l provided n is sufficiently large.

Thus we can say, replacing the measurement of closeness to l i.e. replacing (l-ε ,l+ε ) by (k,∞). Hence the interval I will be (k,∞).

We can say that a_n→∞ as n →∞ iff for every k>0, there exists n₀ ∈ ℕ such that n ≥ n₀ ⟹ an ∈ (k,∞) or a_n > k.

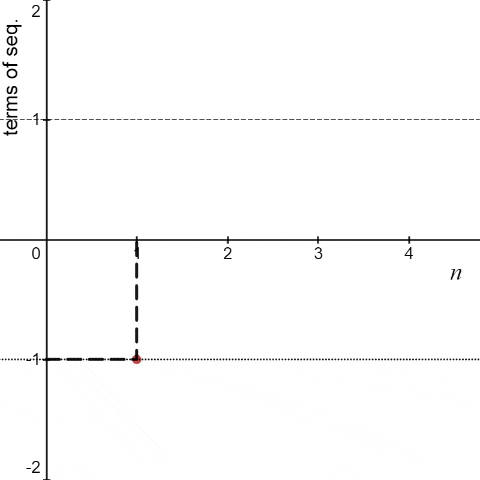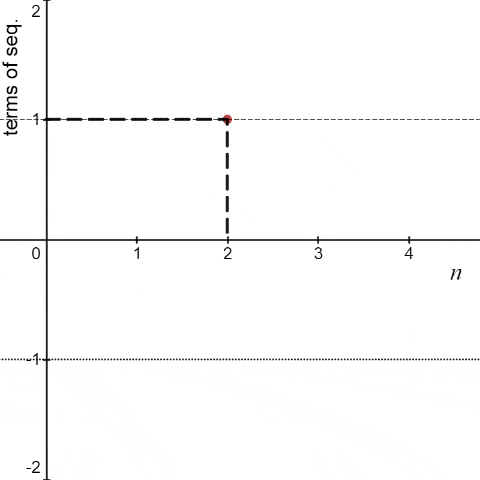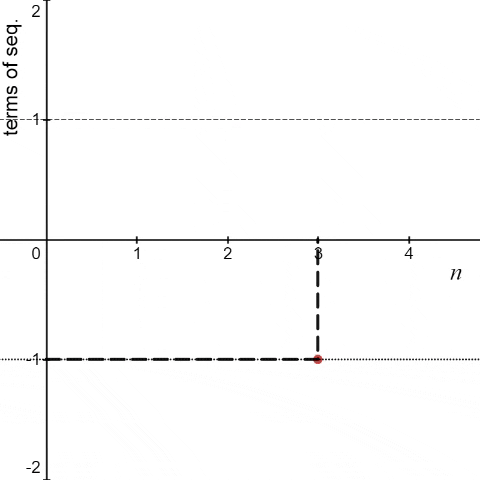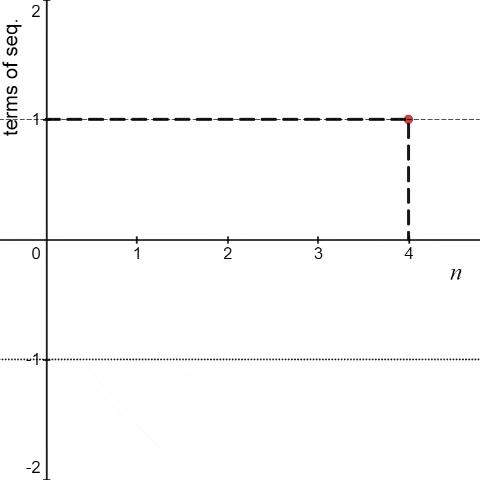
Another example that doesn’t fit the definition  of convergence is <a_n> = (-1)ⁿ  ∀ n.

We can see that the above sequence is neither convergent nor divergent. By the above animation, we can see that the sequence (-1)ⁿ is oscillating between -1 and 1. So, such sequences are called "oscillating" sequences.

Another example of an oscillating sequence can be <a_n> = n(-1)ⁿ ∀ n.

If you notice, this oscillating sequence is not bounded. Such unbounded sequences are said to oscillate infinitely while oscillating sequences like <a_n> = (-1)ⁿ  which are bounded are said to oscillate finitely. 

We hope that this helped you to get a better understanding of real sequences :)

$$
{\displaystyle \mathbb {R} }